Way back in June I won the Greed Tournament, a three week programming competition held by CodeCombat. In part 2 of this series I talked about the unit selection behaviour of my winning solution. This time, I will talk about gold prediction, which allows my solution to forecast the enemy’s future strength and decide whether an attack will succeed.

In part 2, when I talked about the attack behaviour, I mentioned that my code forecasts the enemy’s future strength so that we can know what to expect by the time our army gets to the enemy base. My measure of enemy strength is based on gold — the total gold that they have combined with the total gold value of the military units they currently have on the field.

In order to predict the enemy’s strength at some point in the future, we must be able to estimate how much more gold they are capable of collecting between now and that point. The more accurate this prediction is, the more confident we can be in our attacks.

To do this, I use linear regression. My solution samples the enemy’s cumulative gold (i.e. total gold collected) each turn, using the samples to compute a line of best fit. This is then used to predict how much gold they have at some future time.

Sampling and Prediction

Here is the main code:

// gold prediction main --------------------------------------------------------

if (this.enemyGoldHistory === undefined) {
    this.enemyGoldHistory = [];
}

if (this.counter === undefined) {
    this.counter = 0;
}

var PREDICTOR_HISTORY_LENGTH = 25;
var PREDICTOR_SAMPLE_INTERVAL = 4;
var PREDICTOR_LOOKAHEAD_TIME = 17;

var enemyTotalWorth = 0;
if (enemyBase) {
    enemyTotalWorth = valuateFighters(enemyBase.built) + enemyGold;
}

if (this.counter++ % PREDICTOR_SAMPLE_INTERVAL === 0) {
    this.enemyGoldHistory.push({x: this.now(), y: enemyTotalWorth});
}

if (this.enemyGoldHistory.length > PREDICTOR_HISTORY_LENGTH) {
    this.enemyGoldHistory.shift();
}

var ourMilitaryStrength = valuateFighters(militaryFriends);
var enemyMilitaryStrength = valuateFighters(militaryEnemies);

var ourStrength = ourMilitaryStrength + this.gold;
var enemyStrength = enemyMilitaryStrength + enemyGold;
var enemyStrengthForecast = null;

if (this.enemyGoldHistory.length >= PREDICTOR_HISTORY_LENGTH) {
    var highLowE = estimateHighLow(this.enemyGoldHistory, this.now() + PREDICTOR_LOOKAHEAD_TIME);
    var futureEnemyBonus = highLowE[0] - enemyTotalWorth;

    enemyStrengthForecast = enemyStrength + futureEnemyBonus;
}

Each turn, the enemy’s cumulative gold is computed and assigned to enemyTotalWorth. We determine this by reading how much gold they currently have and adding it together with the gold value of all the units they have built over the game.

Every few turns this value is recorded in enemyGoldHistory against the current time. Once we have enough samples, the function estimateHighLow estimates how much gold the enemy will have at PREDICTOR_LOOKAHEAD_TIME seconds into the future based on the history. The lookahead time, 17 seconds, is about the amount of time it takes for a military unit to walk from our base to the enemy base.

estimateHighLow doesn’t return a single value — it actually returns three values: an upper bound, average, and lower bound estimate. (The main code only actually uses the upper bound, though!) Since the coins spawn randomly, and we don’t know precisely how our opponent’s collection strategy works, there will always be some uncertainty in any estimate we make. The upper bound is a ceiling which we think the opponent will never cross — given their history, we are certain they will not collect more than this much gold. The lower bound is the opposite — we are certain that the opponent will definitely collect at least this much gold.

We use the upper bound value to work out how strong the enemy’s military could be. To do this we simply subtract their current cumulative gold value to find futureEnemyBonus, which tells us how much more gold they will have collected by this time. Then we add this to their current strength, which is simply the gold cost of their living military units combined with their reserve gold.

The Regression Model

The logic I’ve outlined so far does all the grunt work of collecting data and extracting some meaningful information from the prediction, but it all depends upon the prediction function, estimateHighLow, to make accurate forecasts.

Here’s what it looks like

function estimateHighLow(points, time) {
    var regFunc = createRegressionFunc(points);
    
    var deviation = Math.sqrt(estimateVariance(points, regFunc));
    var bound = deviation * 2; // ~95% coverage
    
    var start = regFunc(points[0].x);
    var lowStart = start - bound;
    var highStart = start + bound;
    
    var end = regFunc(points[points.length - 1].x);
    var lowEnd = end - bound;
    var highEnd = end + bound;
    
    var upperBound = lerp(lowStart, highEnd, (time - points[0].x) / (points[points.length - 1].x - points[0].x));
    var lowerBound = lerp(highStart, lowEnd, (time - points[0].x) / (points[points.length - 1].x - points[0].x));
    
    var estimate = regFunc(time);
    
    
    return [upperBound, estimate, lowerBound];
}

The first thing that happens is a bit of higher order function usage. I call createRegressionFunc, which is a function that accepts a bunch of points and returns a new function, representing the line of best fit. This new function accepts an x-axis value (time) and returns the corresponding y-axis value (gold) on the line using the straight line equation y = mx + c. The values of m and c are worked out by createRegressionFunc and “baked in” to the new function before it is returned.

createRegressionFunc works these m and c values out using a simple linear regression formula. I won’t attempt to cover this here — there are plenty of maths websites that list the formula and will do a much better job of explaining it than I can!

Now that we have a function for the line of best fit, we can use it to estimate values. Making a prediction is easy, as we can just plug in the time we want and get out a gold value. The upper and lower bounds are slightly more involved, however.

To determine upper and lower bounds I first calculate the standard deviation of the data. I then use this to draw a new line by offsetting the start and end points by a proportional amount. Hopefully this picture will explain what I mean:

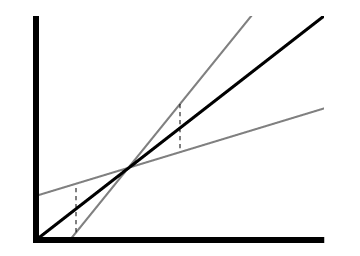
A graph showing a line of best fit with extrapolated upper and lower bounds. The thick black line is the line of best fit, while the two thinner grey lines represent the bounds.

So the calculate the upper bound, I draw a line through lowStart and highEnd, extrapolating into the future to find the required value. The same happens for the lower bound, but with highStart and lowEnd. As we move further into the future the bounds widen, as if to represent the increasing uncertainty of the prediction. The quality and quantity of the data also influences the bounds, as more consistent data, or larger amounts of it, will decrease the standard deviation.

I’m not particularly sure how sound this technique is, since I largely made it up via intuition, but it worked well enough for the competition, so it must be reasonably good!

Closing Remarks

Now you’ve seen how my Greed solution predicts my opponent’s gold income and uses this information to estimate their future military strength. I’ve explained how I used simple linear regression and sample variance to estimate an upper bound on my opponent’s performance, giving my solution confidence in its attacks. This, combined with my previous two blog posts, covers all the components of my Greed strategy.

Since finishing Greed, CodeCombat has run another competition, Criss-Cross, in which players attempt to outbid each other for land in order to form a route across the playing field. I did not compete due to some problems with CodeCombat’s javascript transpiler, but you can read about the solutions of the winners in CodeCombat’s own blog post.

I’ll be sure to keep my eye out for future CodeCombat competitions. I look forward to battling again with other intrepid wizards!